

Kimsuky—also known as VelvetChollima, BlackBanshee, and Thallium—is a North Korean threat actor that has been active since at least 2012. This advanced persistent threat consistently targets South Korean organizations. Its malware arsenal includes modules designed to collect Hangul Word Processor (HWP) documents tied to the Hancom Office software bundle widely used in South Korea.
This threat actor often targets government and defense agencies, research institutes, and non-governmental organizations (NGO), as well as individuals writing on aspects such as North Korean nuclear issues. In early 2019, Kimsuky also conducted campaigns targeting U.S. think tanks. The Cybersecurity and Infrastructure Security Agency (CISA), the FBI, and the U.S. Cyber Command Cyber National Mission Force (CNMF) issued an alert about Kimsuky in 2020.
Our research sheds new light on the encryption mechanism found in various Kimsuky malware samples, including those named Gold Dragon and Ghost419 (see Figure 7 at the end of the blog for representative sample hashes). Open-source reporting does not identify or describe the encryption mechanism. As a member of the Booz Allen Adversary Pursuit cell, we believe that this encryption mechanism—which we call the “Kimsuky cipher”—was invented by the malware authors. The mechanism does not match any publicly known cipher. This blog provides a full description, along with a reference implementation.
Researchers from the Booz Allen Adversary Pursuit cell discovered the Kimsuky cipher while compiling reporting on tactics, techniques, and procedures (TTP) used by the Kimsuky group. We reverse-engineered the cipher from binary samples. Our team has found that Kimsuky typically uses this cipher in conjunction with hard-coded keys. Re-implementation of this cipher allows researchers to decrypt Kimsuky network traffic in real time, providing insight into actor’s TTPs, real-time threat intelligence, and incident response assistance.
The Kimsuky cipher uses a 128-bit key and a 32-bit initialization vector (IV), and functions as a stream cipher. First, there is a key expansion step that sets up the internal state of the cipher. Then, the state of the cipher is advanced outputting one bit at a time, which is masked over the plaintext.
The cipher consists of three shift registers and a lookup table, which functions as an S-box. Two of three shift registers are entirely linear (linear-feedback shift registers or LFSR). The third shift register functions linearly during key expansion but has a non-linear update step during cipher operation. The S-box is initially filled with an alternating sequence of 0’s and 1’s. At each step, two entries of the S-box are swapped. The indices of these entries are selected from a subset of bits from one of the shift registers.
The two open-source ciphers—TRIVIUM and RC4—contain many design similarities to the Kimsuky cipher. TRIVIUM consists of three non-linear feedback shift registers whose output is combined to form the keystream. However, TRIVIUM lacks any form of S-box or permutation table. Also, the S-box used in the Kimsuky cipher is highly similar to the S-box used in RC4, which swaps entries at each step in a similar fashion. Both TRIVIUM and RC4 likely influenced the design on the Kimsuky cipher.
The key and IV are first placed into a 288-bit vector that also contains a run of 128 zeros. This vector is depicted in Figure 1, and will be denoted as 𝑉.
 Figure 1: The 288-bit vector used to initially fill the three shift registers
Figure 1: The 288-bit vector used to initially fill the three shift registers
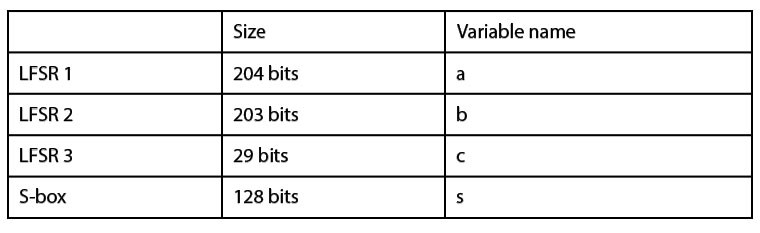 Figure 2: The components that make up the internal state of the cipher, their sizes, and variable names used to reference them
Figure 2: The components that make up the internal state of the cipher, their sizes, and variable names used to reference them
The three LFSRs are initialized to zero and then filled from this vector. The LFSRs, their register sizes, and the variable names used to refer to their internal state are listed in Figure 2. These registers get filled from the vector 𝑉 by iteratively placing a single bit into each LFSR, i.e., 𝑎[0]=𝑣[0], 𝑏[0]=𝑣[1], 𝑐[0]=𝑣[2], 𝑎[1]=𝑣[3], etc. The indices of the shift-registers in which the key is placed are taken modulo the shift register size. This effects LFSR 3 where the initial key bits are overwritten. This means that 42 bits of the 128-bit key have no effect on the final output of the cipher.
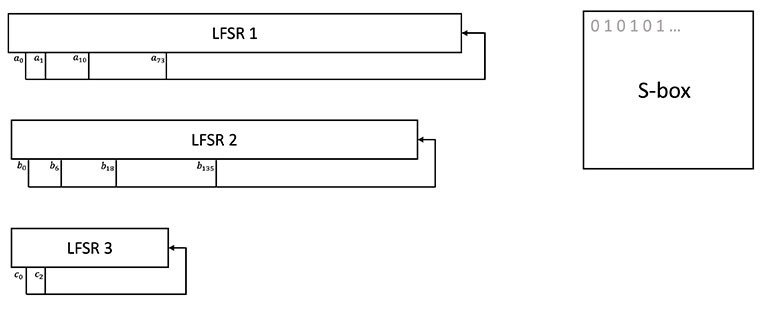 Figure 3: A depiction of the key expansion process. Three LFSRs are filled from the Key and IV and are each stepped out 10,000 cycles after filling. The S-box is initially filled with an alternating sequence of 0’s and 1’s
Figure 3: A depiction of the key expansion process. Three LFSRs are filled from the Key and IV and are each stepped out 10,000 cycles after filling. The S-box is initially filled with an alternating sequence of 0’s and 1’s
After the initial fill, the three LFSRs are stepped out by 10,000 steps. The shift registers, also depicted in Figure 3, are defined by the following polynomials over GF(2):
LFSR1: a204 + a203 + a194 + a131 + 1
LFSR2: b203 + b197 + b185 + b68 + 1
LFSR3: c29 + c27 + 1
The 128-bit S-box is simply filled with the recurring pattern “0 1 0 1 0 1…”.
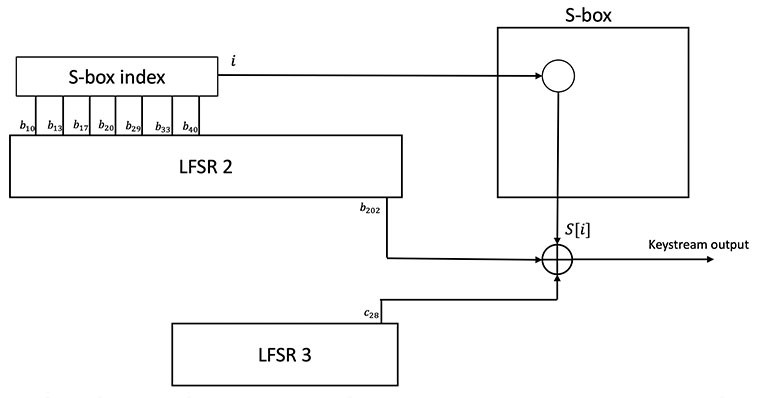 Figure 4: The keystream generation. A single bit is selected out of the S-box based on an index generated out of the registers of LFSR2. This bit is XOR’ed with a register from LFSR2 and a register from LFSR3 to form the keystream
Figure 4: The keystream generation. A single bit is selected out of the S-box based on an index generated out of the registers of LFSR2. This bit is XOR’ed with a register from LFSR2 and a register from LFSR3 to form the keystream
The process for retrieving a bit of keystream during the normal operation of the cipher is depicted in Figure 4. Seven bits are selected out of LFSR 2 and used as an index in the S-box. Specifically, the index selected from the following bits, listed from least significant to most significant order: 𝑏[40], 𝑏[33], 𝑏[29], 𝑏[20], 𝑏[17], 𝑏[13], 𝑏[10]. The S-box entry at this position is then XOR’ed with the bits 𝑏[202] and c[28], from LFSRs 2 and 3, respectively, to form the keystream output.
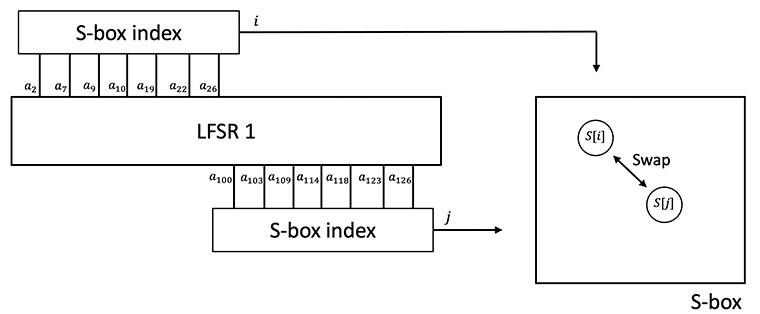 Figure 5: The S-box update process. Two values from the S-box are swapped. The indices for these values are generated from registers in LFSR2
Figure 5: The S-box update process. Two values from the S-box are swapped. The indices for these values are generated from registers in LFSR2
After each bit of output, the state of the cipher is advanced. The first step in the process, depicted in Figure 5, is to swap two entries in the S-box. The index of these two entries is selected using bits from LFSR 1. The first index is selected using the following bits, listed from least significant to most significant order: 𝑎[26], 𝑎[22], 𝑎[19], 𝑎[10], 𝑎[9], 𝑎[7], 𝑎[2]. The second index is selected using the bits 𝑎[126], 𝑎[123], 𝑎[118], 𝑎[114], 𝑎[109], 𝑎[103], 𝑎[100].
Following the S-box update, the three shift registers are stepped out once in between keystream outputs. LFSRs 1 and 3 are operate entirely linearly according to the process described during key expansion. Shift register 2 contains a non-linear component that takes input from shift register 1. Note that this input is computed before LFSR1 is advanced. This step is depicted in Figure 5, where symbol denotes a binary AND, and the symbol
denotes a binary XOR. The non-linear input from LFSR1 can be described by the equation (a[20]
a[30])
(a[55]
(a[20]
a[30])).
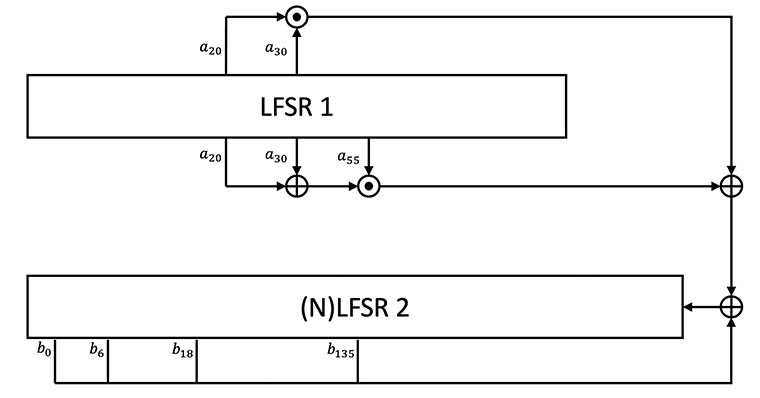 Figure 6: The non-linear update step for LFSR2 used during cipher operation. A non-linear combination of bits from LFSR1 is fed into the input of (the now non-linear) LFSR2
Figure 6: The non-linear update step for LFSR2 used during cipher operation. A non-linear combination of bits from LFSR1 is fed into the input of (the now non-linear) LFSR2
| fa0b1aa8ff08df4ad254fde218d0b7a8e776d2cda27c4310af338a7b022b6559 |
| a620434b2efc48ec46b5a618e269936cef984ad98cb33d5a656ae1a9eef7362f |
| fe7327bf67e37cb1a581868010034a4009c298ea73977deed4bb0fa781dace0f |
| 22585b1bc8a43130c2cb4ab03ed7cf2eae20a6364caecbefa31945b7a34f28ff |
| 25a1f1294a51ea92403605b93f7b808b489206d87561ca04cb7b6d3fdc98fc7e |
| c54837d0b856205bd4ae01887aae9178f55f16e0e1a1e1ff59bd18dbc8a3dd82 |
| 639cdfab319af1f9d064ac08f03f990a4a0702ccc07b47538751ce6e5214c95b |
| 891913a89896932dc04caae096e46ebcf8ffbb7c55fdfe7fc5f272ed9354a76c |
| bfb8d13fcb64e3d09de2850b47d64492dbfc7bba58766546c1511f1fa59a64c9 |
| 4ff2a67b094bcc56df1aec016191465be4e7de348360fd307d1929dc9cbab39f |
| b1e28bc8720303326946ec69d8ad6c90b572e177d562bbe769abaf1aad3d9e1a |
| 8f2cbc93b7cd5cdc54e1670105c3da682bae0b70bc6bc4b0c0c18ab5c40be9c4 |
Figure 7: Samples using this cipher (SHA256 hashes)
def bytes_to_bits( in_bytes ):
out = b''
for b in in_bytes:
for i in range(8):
t = (b >> i) & 1
out += t.to_bytes(1,'little')
return out
def bits_to_bytes( in_bytes ): if len( in_bytes ) % 8 != 0: raise ValueError() out = b'' for i in range(int(len(in_bytes)/8)): byte = 0 for j in range(8): byte += in_bytes[8*i+j] << j out += byte.to_bytes(1,'little') return out class kimsuky_cipher: #LFSR registers r1 = bytearray(204) r2 = bytearray(203) r3 = bytearray(29)
sbox = bytearray(128)
def __init__( self, key, iv ):
'''
This is the key expansion algorithm. First fill a buffer with
[ 128-bit key | 128-bits of zero | 32-bits of IV ]
'''
if len(key) != 16 and len(iv) != 8:
raise ValueError()
key = bytes_to_bits( key )
iv = bytes_to_bits( iv )
t = key + bytes(128) + iv
#bit 0 -> lfsr1 bit 0
#bit 1 -> lfsr2 bit 0
#bit 2 -> lfsr3 bit 0
#bit 4 -> lfsr1 bit 1
# etc
for i, b in enumerate(t):
j = int(i/3)
if i % 3 == 0:
self.r1[ j % 204 ] = t[i]
elif i % 3 == 1:
self.r2[ j % 203 ] = t[i]
else:
self.r3[ j % 29 ] = t[i]
#initialized as 0 1 0 1 ...
for i in range(128):
self.sbox[i] = i % 2
#run out each lfsr 10000x
for i in range(10000):
b = self.r1[0] ^ self.r1[1] ^ self.r1[10] ^ self.r1[73]
self.r1[0:-1] = self.r1[1:]
self.r1[-1] = b
b = self.r2[0] ^ self.r2[6] ^ self.r2[18] ^ self.r2[135]
self.r2[0:-1] = self.r2[1:]
self.r2[-1] = b
b = self.r3[0] ^ self.r3[2]
self.r3[0:-1] = self.r3[1:]
self.r3[-1] = b
def keystream( self, n_bytes ):
n_bits = 8*n_bytes
out_bits = bytearray(n_bits)
for i in range(n_bits):
out_bits[i] = self.next_bit()
return bits_to_bytes( out_bits )
def next_bit( self ):
#get a byte from r2 and use it to pick an entry out of the sbox
byte_from_r2 = (self.r2[40]) | (self.r2[33] << 1) | (self.r2[29] << 2) | (self.r2[20] << 3)
byte_from_r2 |= (self.r2[17] << 4) | (self.r2[13] << 5) | (self.r2[10] << 6)
s_byte = self.sbox[ byte_from_r2 ]
#combine with output from r2 and r3 to make cipher bit
mask_bit = s_byte ^ self.r3[28] ^ self.r2[202]
self.__advance_state()
return mask_bit
def __advance_state( self ):
#get two bytes from r1 and use them to select to sbox locations
b1 = (self.r1[26]) | (self.r1[22] << 1) | (self.r1[19] << 2) | (self.r1[10] << 3)
b1 |= (self.r1[9] << 4) | (self.r1[7] << 5) | (self.r1[2] << 6)
b2 = (self.r1[126]) | (self.r1[123] << 1) | (self.r1[118] << 2) | (self.r1[114] << 3)
b2 |= (self.r1[109] << 4) | (self.r1[103] << 5) | (self.r1[100] << 6)
#swap the two locations
self.sbox[ b1 ], self.sbox[ b2 ] = self.sbox[ b2 ], self.sbox[ b1 ]
#lfsr 2 has a non-linear input from r1
b = self.r1[20] ^ self.r1[30]
b &= self.r1[55]
b ^= self.r1[20] & self.r1[30]
b ^= self.r2[0] ^ self.r2[6] ^ self.r2[18] ^ self.r2[135]
self.r2[0:-1] = self.r2[1:]
self.r2[-1] = b
#step out lfsr 1 and 3 as normal
b = self.r1[0] ^ self.r1[1] ^ self.r1[10] ^ self.r1[73]
self.r1[0:-1] = self.r1[1:]
self.r1[-1] = b
b = self.r3[0] ^ self.r3[2]
self.r3[0:-1] = self.r3[1:]
self.r3[-1] = b
Figure 8: Python implementation of cipher
This blog series is brought to you by Booz Allen DarkLabs. Our DarkLabs is an elite team of security researchers, penetration testers, reverse engineers, network analysts, and data scientists, dedicated to stopping cyber attacks before they occur.
This article is for informational purposes only, its content may be based on employees’ independent research, and does not represent the position or opinion of Booz Allen. Furthermore, Booz Allen disclaims all warranties in the article's content, does not recommend/endorse any third-party products referenced therein, and any reliance and use of the article is at the reader’s sole discretion and risk.